Photo by Roman Mager on Unsplash

Pre-processing and cleaning data are important tasks that must be conducted before a dataset can be used for model training. Raw data is often noisy and unreliable, and may be missing values. Using such data for modeling can produce misleading results.

Below are the common methods for pre-processing and cleaning your data:

Normalization

Data normalization rescales numerical values to a specified range. Popular data normalization methods include:

• Min-Max Normalization: Linearly transform the data to a range, say between 0 and 1, where the min value is scaled to 0 and max value to 1.

• Z-score Normalization: Scale data based on mean and standard deviation: divide the difference between the data and the mean by the standard deviation.

• Decimal scaling: Scale the data by moving the decimal point of the attribute value.

Normalization usually rescales features to [0, 1][0,1].1 That is,

x’ = \dfrac{x — min(x)}{max(x) — min(x)}x′=max(x)−min(x)x−min(x)​

It will be useful when we are sure enough that there are no anomalies (i.e. outliers) with extremely large or small values. For example, in a recommender system, the ratings made by users are limited to a small finite set like \{1, 2, 3, 4, 5\}{1,2,3,4,5}.

In some situations, we may prefer to map data to a range like [-1, 1][−1,1] with zero-mean.2 Then we should choose mean normalization.3

x’ = \dfrac{x — mean(x)}{max(x) — min(x)}x′=max(x)−min(x)x−mean(x)​

In this way, it will be more convenient for us to use other techniques like matrix factorization.

Standardization

Standardization is widely used as a preprocessing step in many learning algorithms to rescale the features to zero-mean and unit-variance.3

x’ = \dfrac{x — \mu}{\sigma}x′=σx−μ​

Regularization

Different from the feature scaling techniques mentioned above, regularization is intended to solve the overfitting problem. By adding an extra part to the loss function, the parameters in learning algorithms are more likely to converge to smaller values, which can significantly reduce overfitting.

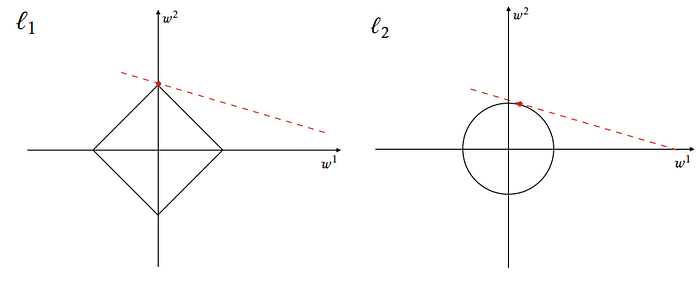
There are mainly two basic types of regularization: L1-norm (lasso) and L2-norm (ridge regression).4

L1-norm5 — Lasso Regularization

• Shrinks coefficients of less important features to zero and removes them

• Good for feature selection when dataset has a large number of features

• Generates simpler models

• Robust to outliers

The original loss function is denoted by f(x)f(x), and the new one is F(x)F(x).

F(x) = f(x) + \lambda {\lVert x \rVert}_1F(x)=f(x)+λ∥x∥1​

where

{\lVert x \rVert}_p = \sqrt[p]{\sum_{i = 1}^{n} {\lvert x_i \rvert}^p}∥x∥p​=pi=1∑n​∣xi​∣p​

L1 regularization is better when we want to train a sparse model, since the absolute value function is not differentiable at 0.

L2-norm56 — Ridge Regularization

• Shrinks parameters but does not remove them

• Performs better when model depends on all features

• Has no feature selection

• Not robust to outliers

F(x) = f(x) + \lambda {\lVert x \rVert}_2²F(x)=f(x)+λ∥x∥22​

L2 regularization is preferred in ill-posed problems for smoothing.

Here is a comparison between L1 and L2 regularizations.

From en.wikipedia.org/wiki/Regularization_(mathe..